Quando se pensa em experimentos científicos inerentemente vem o conceito de confiabilidade. Para ilustrar a questão, vamos pensar num elemento conhecido, tendo a confiabilidade como sua característica principal. Se numa embalagem de preservativo há uma inscrição do tipo: “Mais ou menos 98% seguro” e em outra: “Testados eletronicamente um a um, 99,9% seguro”, qual das duas naturalmente todos escolheriam!? Óbviamente a segunda. Esse exemplo pode parecer exagerado, mas ilustra bem a questão. Nos experimentos, envolvendo aplicações matemáticas os algarismos significativos são indicadores dos erros presentes na representação de um dado.
Algarismos Significativos
Tomemos como exemplo a medição da temperatura ambiente em um dado local. No primeiro caso, o dado obtido é 21,0ºC, enquanto que para o segundo, o dado é 20,972ºC. Para o primeiro caso, não se tem realmente certeza se o algarismo “0” é correto. Este algarismo é então chamado de algarismo duvidoso, pois pode-se ter por exemplo tanto 20,9ºC ou 21,1ºC, ou seja, se admite erros neste algarismo, então dizemos que o dado tem 2 algarismos significativos. Essa variação pode ocorrer por erros de tomada de dados, ou até mesmo arredondamentos.
Para o segundo caso, têm-se uma medida com mais algarismos significativos, o que significa que se aproxima mais do valor real, ou seja, o valor é mais confiavel. A importancia do número de algarismos significativos a serem adotados depende normalmente do tipo de experimento e consequentemente do grau de precisão dos instrumentos utilizados e o detalhamento dos modelos matemáticos a serem empregados.
Algarismos significativos são utilizados para minimizar os erros de arredondamento. Quanto maior o número de algarismos significativos, maior é a certeza envolvida na medida. Entede-se por significativo o fato do número ter um significado real, normalmente relacionado a um efeito físico. Por exemplo, a constante π (pi) tem infinitos algarismos, mas terá o número de algarismos significativos de acordo com a precisão da calculadora que é utilizada ou com a precisão desejada num determniado cálculo.
Precisão e Exatidão
Um sistema de medições é dito exato, se ao realizar uma série de medições o valor médio desta série correspondente ao valor real. Ainda que haja desvio padrão elevado na série o sistema é dito exato. Caso o valor médio encontrado seja muito diferente do valor real, porém o desvio padrão da série seja muito baixo o sistema é chamado de preciso.
O objetivo então é aproximar-se o máximo possível de um sistema preciso e exato, pois é desejável obter leituras de dados próximos entre si e próximos ao valor real.
As ilustrações facilitam o entendimento:
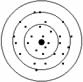
Exato e não Preciso
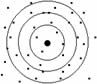
Nem Exato e Nem Preciso
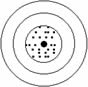
Preciso e Exato
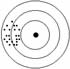
Preciso e não Exato
Interpolação
Interpolação é um método que possibilita gerar um novo conjunto de dados a partir de dados pontuais conhecidos. Em exprimentos científicos, usualmente dispõe-se de dados pontuais, que são os dados coletados em amostragem, por exemplo. Com o uso de técnicas de interpolação é possível construir uma nova função que tenha o objetivo de simplificar a função original, considerando aproximações dos dados pontuais.
Dessa forma, tem-se funções mais simples, oriundas de funções complexas que seriam de manipulação inviavel. Contudo ao adotar essa prática deve-se ter em mente o grau de aproximação que foi adotado e deve estar claro que caso sejam gerados novos dados através de calculos utilizando estas novas funções haverá discrepancia entre os mesmos e os dados pontuais originais.
Deve ser avalido o grau de simplificação que será adotado para que o inerente erro que acompanhará a simplificação não comprometa o trabalho em questão.
Medições Diretas e Indiretas
A diferenciação que pode ser feita para as medidas de grandezas físicas relaciona-se com a forma de obtenção dessa grandeza. Usualmente difere-se os dados em medidos de forma direta e indireta.
As chamadas medidas diretas para uma grandeza física são sempre resultado de leituras de uma propriedade com auxilio de um instrumento de medição. Exemplificando: ao se tomar as medidas de comprimento e largura do tampo de uma mesa, utilizando uma régua graduada são obtidas medidas diretas. Um outro exemplo é a leitura da variação da queda de tensão em componentes de um circuito elétrico ao adicionar resistencias no mesmo.
Já as medidas indiretas são resultado da utilização de expressoes matemáticas, que venham a relacionar grandezas diretas ou indiretas. Exemplificando: O valor da velocidade média de um corredor durante determinado percurso, será dado pela razão entre o espaço percorrido por ele (grandeza direta) e o tempo decorrido no percurso (grandeza direta).