<h2>Função Exponencial</h2>
<p align=”left”>Na <a href=”http://www.somatematica.com.br/”>matemática</a> existem vários tipos de funções que são imprescindíveis para a determinação de diversos cálculos, e seu conceito é uma generalização do senso comum sobre uma fórmula de matemática. As funções então descrevem as relações especiais entre 2 objetos, que são denominados de “x” e “y” sob o <a href=”//www.culturamix.com/marketing/criativo/pontos-de-vista”>ponto de vista</a> matemático. Assim “x” passa a ser designado de argumento ou mesmo de domínio da função “f”, enquanto “y” que sempre depende de “x” é designado de imagem de “x” pela “f”. enfim, uma função é então uma forma utilizada para associar um valor único da função “f(x)” a cada valor do domínio da função “x”. Isso pode ser feito de várias formas, utilizando-se uma formula matemática, um relacionamento gráfico entre os diagramas em que se represente os 2 conjuntos, também pode ser feito através de uma regra de associação e também pode ser construída uma tabela de correspondência. A representação das funções através de gráficos é muito comum quando se trata de conjuntos numéricos.</p>
<h2>Surgimento das Funções</h2>
<p align=”left”>Foi em 1694 que o matemático Leibniz introduziu o termo “função” nos seus tratados matemáticos, que então era utilizado para descrever as quantidades que estavam relacionadas a uma determinada curva, seja um ponto específico da curva ou mesmo a inclinação desta mesma <a href=”//www.culturamix.com/dinheiro/economia/curva-de-crescimento-em-debate”>curva</a>. Os conceitos matemáticos também evoluíram com o tempo e a essas funções foi dado o nome de funções diferenciáveis, até que no século XVIII o matemático Euler passou a usar a expressão “função” para descrever expressões matemáticas que usassem diversos argumentos. A princípio essas funções foram tidas como imaginárias e fictícias, no entanto já no século XX, sua utilidade foi identificada, e se tornaram importantes para muitos fins, especialmente para a construção de modelos de fenômenos físicos, tal qual o movimento de Brown. Mas foi o matemático Dirichlet quem estabeleceu a definição de função, tal qual a conhecemos hoje. São diversas as funções, entre elas destacamos o estudo das funções exponenciais.</p>
<h2>Definição, Características e Utilidades das Funções Exponenciais</h2>
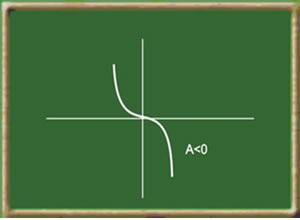
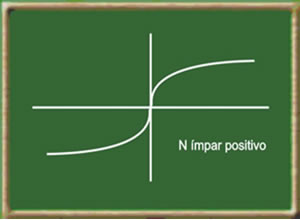
<p align=”left”>As funções exponenciais são definidas com sendo inversas das funções de <a href=”//www.culturamix.com/cultura/escolar/logaritmos”>logaritmos</a> normais, e se caracterizam por crescerem e decrescerem muito rapidamente. Assim a função exponencial é muito utilizada tanto na própria matemática como também nas demais ciências que se interligam a matemática como a Química, a Física, a <a href=”//www.culturamix.com/cultura/curiosidades/astronomia”>Astronomia</a>, a Engenharia, a Biologia, a Geografia, a Economia e outras ciências onde os cálculos matemáticos tem papel importante. Como exemplos da utilização das funções exponenciais na prática, podemos citar por exemplo na geografia para determinar os índices de crescimento da população, na Biologia seu uso é fundamental também para determinar o rápido crescimento das colônias de bactérias, na química seu uso é indicado para o calculo do decaimento radioativo. </p>
<p align=”left”>Já na matemática financeira pode ser utilizado para estabelecer o crescimento de um investimento com uma taxa de juros determinada. Como suas curvas enquadram situações de crescimento e decrescimento, também permitem o estudo do desempenho e da aprendizagem dos alunos e qualquer outra avaliação de crescimento ou decrescimento que se deseje efetivar. As funções exponenciais são um conteúdo muito importante da <a href=”//www.culturamix.com/cultura/escolar/olimpadas-de-matematica”>matemática</a> do ensino médico, muito solicitado em provas de concursos e também em <a href=”//www.culturamix.com/cultura/escolar/vestibular”>vestibulares</a> e sua aplicação também é requisitada no desempenho de diversas profissões, por isso, apesar de parecer um pouco complicado a princípio, com muitos exercícios e a prática o seu aprendizado se torna prazeroso e estimulante, pois desafia e aguça nosso raciocínio.</p>
Função Exponencial
Na matemática existem vários tipos de funções que são imprescindíveis para a determinação de diversos cálculos, e seu conceito é uma generalização do senso comum sobre uma fórmula de matemática. As funções então descrevem as relações especiais entre 2 objetos, que são denominados de “x” e “y” sob o ponto de vista matemático. Assim “x” passa a ser designado de argumento ou mesmo de domínio da função “f”, enquanto “y” que sempre depende de “x” é designado de imagem de “x” pela “f”. enfim, uma função é então uma forma utilizada para associar um valor único da função “f(x)” a cada valor do domínio da função “x”. Isso pode ser feito de várias formas, utilizando-se uma formula matemática, um relacionamento gráfico entre os diagramas em que se represente os 2 conjuntos, também pode ser feito através de uma regra de associação e também pode ser construída uma tabela de correspondência. A representação das funções através de gráficos é muito comum quando se trata de conjuntos numéricos.
Função Exponencial
Surgimento das Funções
Foi em 1694 que o matemático Leibniz introduziu o termo “função” nos seus tratados matemáticos, que então era utilizado para descrever as quantidades que estavam relacionadas a uma determinada curva, seja um ponto específico da curva ou mesmo a inclinação desta mesma curva. Os conceitos matemáticos também evoluíram com o tempo e a essas funções foi dado o nome de funções diferenciáveis, até que no século XVIII o matemático Euler passou a usar a expressão “função” para descrever expressões matemáticas que usassem diversos argumentos. A princípio essas funções foram tidas como imaginárias e fictícias, no entanto já no século XX, sua utilidade foi identificada, e se tornaram importantes para muitos fins, especialmente para a construção de modelos de fenômenos físicos, tal qual o movimento de Brown. Mas foi o matemático Dirichlet quem estabeleceu a definição de função, tal qual a conhecemos hoje. São diversas as funções, entre elas destacamos o estudo das funções exponenciais.

Exercício
Definição, Características e Utilidades das Funções Exponenciais
As funções exponenciais são definidas com sendo inversas das funções de logaritmos normais, e se caracterizam por crescerem e decrescerem muito rapidamente. Assim a função exponencial é muito utilizada tanto na própria matemática como também nas demais ciências que se interligam a matemática como a Química, a Física, a Astronomia, a Engenharia, a Biologia, a Geografia, a Economia e outras ciências onde os cálculos matemáticos tem papel importante. Como exemplos da utilização das funções exponenciais na prática, podemos citar por exemplo na geografia para determinar os índices de crescimento da população, na Biologia seu uso é fundamental também para determinar o rápido crescimento das colônias de bactérias, na química seu uso é indicado para o calculo do decaimento radioativo.
Logarítmica
Já na matemática financeira pode ser utilizado para estabelecer o crescimento de um investimento com uma taxa de juros determinada. Como suas curvas enquadram situações de crescimento e decrescimento, também permitem o estudo do desempenho e da aprendizagem dos alunos e qualquer outra avaliação de crescimento ou decrescimento que se deseje efetivar. As funções exponenciais são um conteúdo muito importante da matemática do ensino médico, muito solicitado em provas de concursos e também em vestibulares e sua aplicação também é requisitada no desempenho de diversas profissões, por isso, apesar de parecer um pouco complicado a princípio, com muitos exercícios e a prática o seu aprendizado se torna prazeroso e estimulante, pois desafia e aguça nosso raciocínio.